Cargo airships could be big… but if they're too big they'll get ripped apart by turbulence

People are starting to agree that cargo airships could be big.

Large airships might offer joule/ton-km transport costs close to seagoing cargo ships, but with delivery times closer to airplanes, and more flexibility to deliver cargo point-to-point than either one.

The key would be scale. On an airship, the lifting capacity is proportional to the volume of gas in its hull (L³). The drag is proportional to the cross-sectional area (L²). Consequently, as airships get larger, the cost per ton-km to move goods might decrease almost linearly. At a certain scale, this advantage presumably builds to the point where other concerns (inability to fly above weather, people making Hindenburg jokes etc.) seem like small issues.

But how far does this scaling logic go? Since airships aren’t limited by the size of canals or ports, would economics push us towards stadium-sized airships? City-sized airships?

The actual physical limit might come from a surprising place: the wind. Here, we look at atmospheric correlation lengths and spitball the maximum size for any buoyant vessel that could stay aloft without being torn apart by differential forces due to turbulent air.

The square-cube law is a common and frequently powerful piece of received wisdom: where the benefits of a system accrue with its surface area but the demerits accrue to the volume, it’s best to make the system as small as practical – something appreciated as much by lovers of the crunchy edge of a brownie as by the designers of microscopic chemical catalysts. For other systems, the reverse is true, and it makes sense to build things as large as possible: chemical reactors, gas turbines, and big fat polar bears weathering the arctic night all benefit from a 2D term (heat loss etc.) diminishing relative to a 3D term (heat generation etc.) with increasing size^[1].

This sort of benefit with scaling isn’t limited to thermal and chemical diffusion. It also holds for fluid viscosity, which acts to diffuse momentum – viscous drag. At human scales, drag from viscosity in air and water accumulates in a thin boundary layer at the surface of a boat or aircraft and diminishes relative to other forces as the vessel increases in size. Cargo ships and other buoyant vessels show this especially straightforwardly, with buoyancy and cargo capacity accumulating with volume but viscous drag limited by the surface area.  Humanity therefore builds these vessels to the max^[2]—limited only by the sizes of ports, canals, and waterways in which they can operate.

Dirigibles and other airships also rely on buoyancy. Does it make sense to make them as large as possible?

The naïve answer is “of course it does”. The Hindenburg and Graf Zeppelin, after all, were the largest flying machines ever built^[3]. But it’s worth thinking a little bit more about how strong we have to make the structure of an airship for it to survive in the prevailing conditions. If the structure needs to get heavier more than linearly as the length of the airship increases, we don’t gain anything from greater scale.

What determines the strength of the envelope an airship needs? For all sorts of air- and surface-craft, loads on the skin come partly from “static” pressure and partly from "dynamic” pressure. Static pressure refers to forces the vessel would experience even if it weren’t moving. Static loads result from some characteristic common to the whole vessel: the draft of a boat, the size of a lighter-than-air craft, the pressurization loads for airliners; these loads are predictable and fairly constant over the size of the vehicle and course of the trip. Dynamic pressure by contrast represents the forces exerted to move the fluid around the vessel’s shape; since the fluid moves faster in some places and slower in others the dynamic pressure varies over the vehicle and varies in time with the velocity field of the fluid that the vehicle moves through. For an aerial vehicle, airspeed and wind variability (turbulence) are the main drivers of dynamic pressure loads^[4].

We can make some comparisons:

Uniquely for the dirigible, the dynamic forces dominate the static ones. This suggests that an understanding of the motion of an airship and the turbulence it experiences will inform the design of an airship to a much greater extent than with ships or airplanes.

Let’s look specifically into the loads an air vehicle experiences due to turbulence. Both lighter- and heavier-than-air aircraft are designed to accommodate gusts and turbulence by considering how the structure responds as it moves through a “frozen” profile of wind, usually specified in separate vertical and horizontal components.

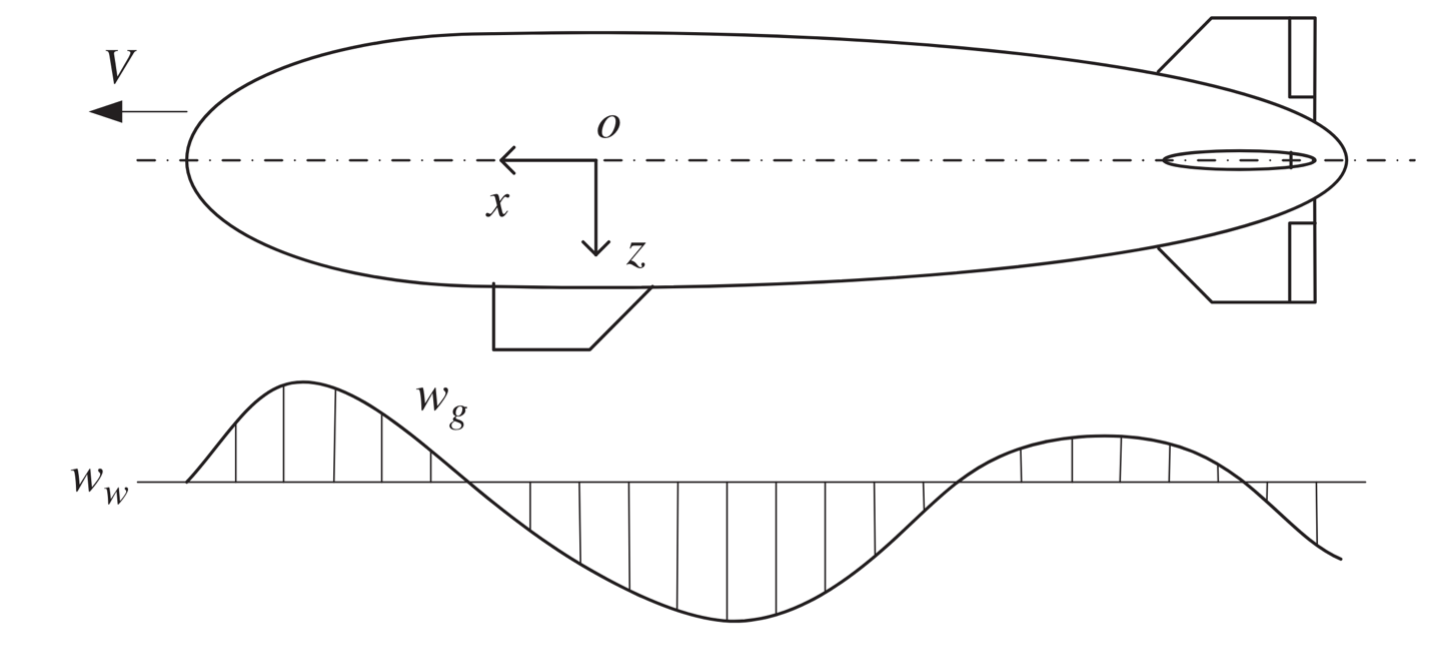
The shape and strength of the profile both affect how a structure responds: variation with a length scale close to the size of the vehicle generally results in the largest net accelerations and structural loads, while variation much smaller may vibrate the structure or controls without displacing the vehicle. Variation much larger than the scale of the vehicle might result only in slow trim or speed changes. Profiles are specified in the airworthiness standards for both transport aircraft [1] and airships [7] as both “discrete gusts” with a particular shape and as random turbulence generated by a model like the von Karman model. These profiles aren’t recordings of real gusts; they’re generated to safely bound the gusts recorded in surprisingly-identical experiments in aircraft ranging from an Aeronca [9] to an XB-70 [10].

Discrete gusts have a “1-wave cosine” spatial profile and peak intensity that increases with the spatial size of the gust to the 1/6 power. Reflecting the more conservative risk posture and wider variety of conditions in which transport-category aircraft – the category of aircraft that can be used in commercial airline service – are used, the gust profiles used to design transport aircraft are about 80% stronger than those for airships, though their scaling is the same.

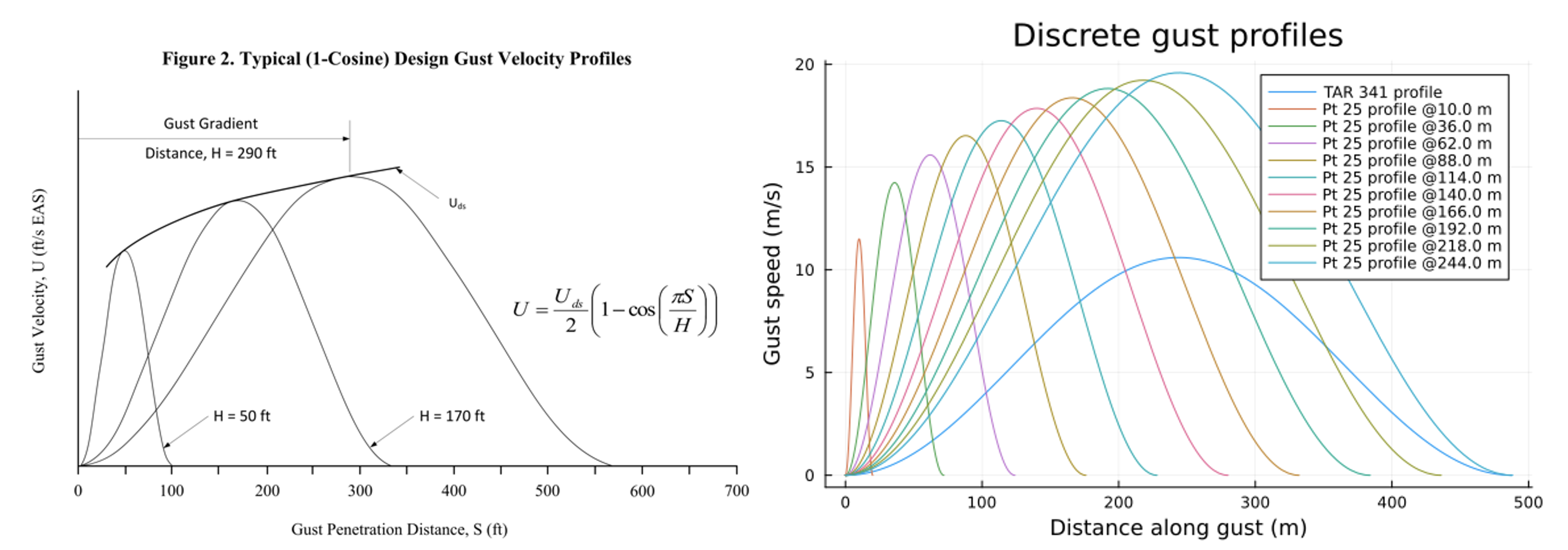
Aircraft designers are encouraged to consider the effects of “gust gradient distances” up to slightly beyond the size of their aircraft. That’s because the peak bending moment an aircraft will experience as it traverses turbulent air will scale with the square of distance from the center of mass. For a particular ratio of length to radius, the skin thickness required to avoid buckling of a cylindrical shell is linear in the applied moment [11]. Summing it up illustrates an under-appreciated difficulty for large airships^[5]:

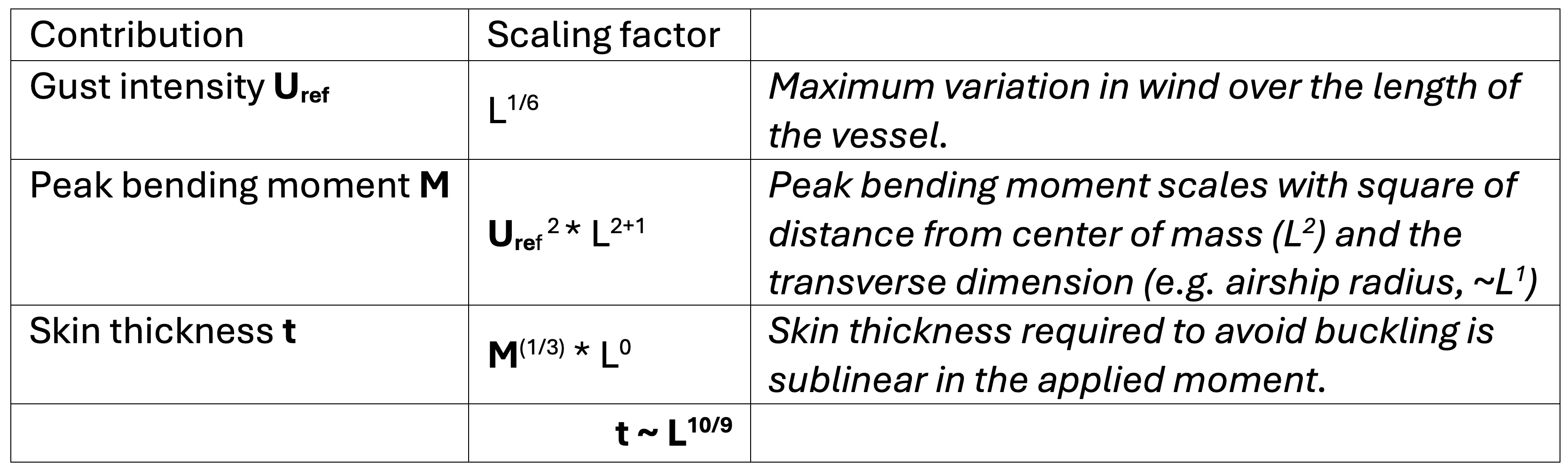
A t ~ L^10/9 scaling in the skin thickness is larger than the linear scaling we’d hope for.  That strongly indicates that aircraft larger than the largest gust gradient distances of 100 meters or so contemplated by existing regulation are likely to find their structures limited by a different kind of gust altogether.

To resummarize thus far: While the load-carrying capacity of a theoretical airship increases linearly with its length in calm air, once an airship grows to span bodies of air moving in different directions, the thickness of the airframe required to withstand discrete gusts grows at the 10/9 power. That suggests that above a certain size, the load-carrying capacity of an airship no longer increases but rather decreases with scale, since the airship structure has to be made heavier to survive the wind loads it will encounter.

That's the story for discrete gusts. Things get more complicated when we consider actual turbulence models^[6].

The gust profiles generated by models like the von Karman wind turbulence model are intended to represent worst cases of severe turbulence encountered on a “continuous” basis, with the airplane and its control system able to operate safely in quasi-equilibrium in the wind field that these models generate. These turbulence models are primarily characterized by an overall intensity (σ, the standard deviation over space of the velocity) and a length scale. At points much farther apart than the length scale, the velocities are uncorrelated; much closer, and the velocities are correlated. Unsurprisingly, the wind fields these models generate look a lot like clouds, as in this typical example of continuous surface-level continuous turbulence (σ = 27 m/s = 90 feet/s, as in 14 CFR 25.341) - Hindenburg for scale:

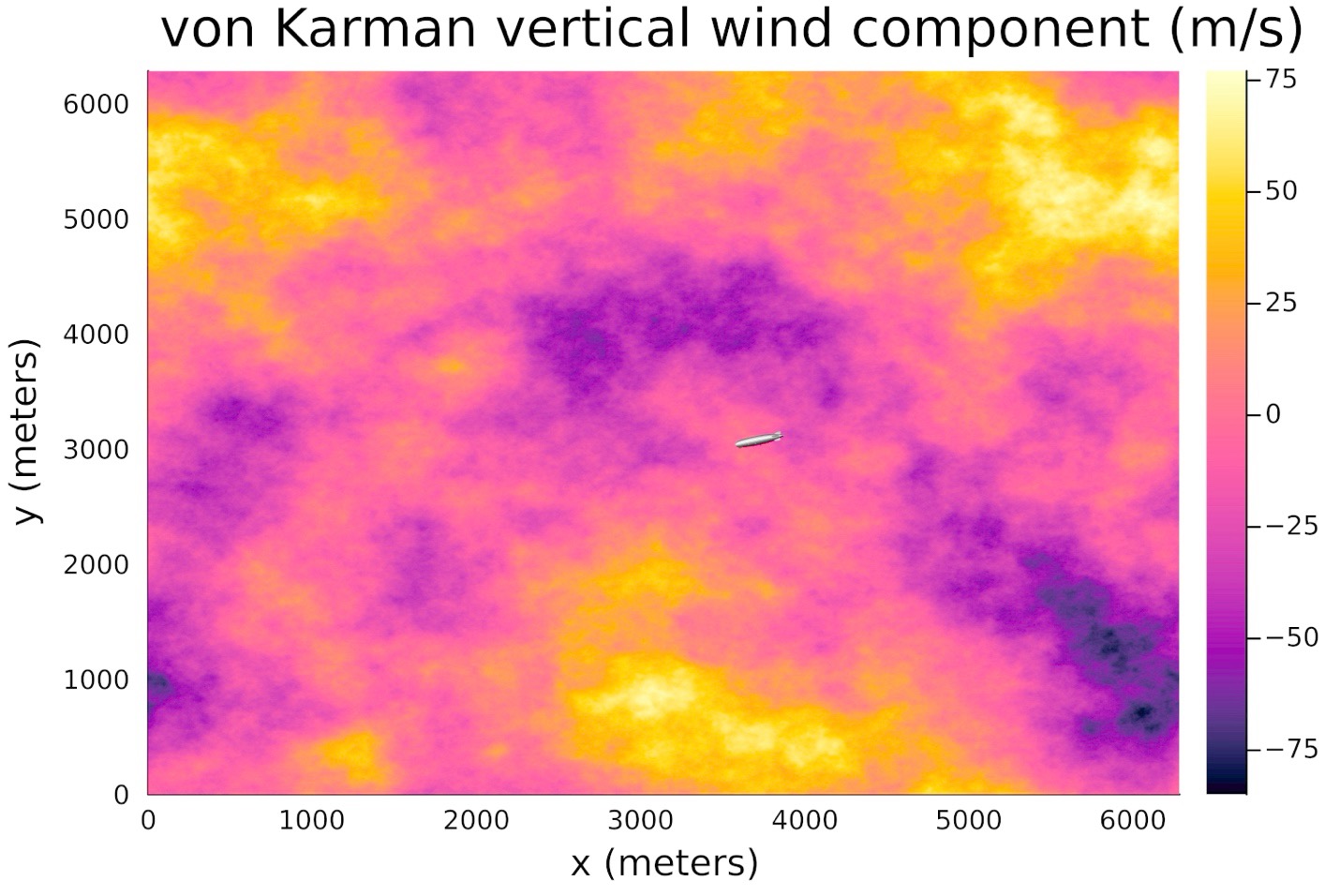
Turbulence models used in different aeronautical applications have length scales between 400 and 800 meters; in practice this means that the gust loads imparted will scale slowly below this length, quickly near the length, and remain similar beyond it. An aircraft with a largest dimension 2 km or above traversing an area of severe turbulence like this would be expected to frequently encounter differences in vertical wind speed across its surface of 6σ or more, a load encountered by smaller aircraft with exponentially low probability. While there’s no neat scaling power we can apply at all scales for continuous turbulence, the exponential scaling of structural loads near the turbulence characteristic length will probably prevent aircraft from getting much larger than that.

We can circle back to the structural comparison we began the discussion with by asking the question more concretely: between different sizes of dirigible, how frequently does the continuous gust structural load exceed the load imposed by the cargo?

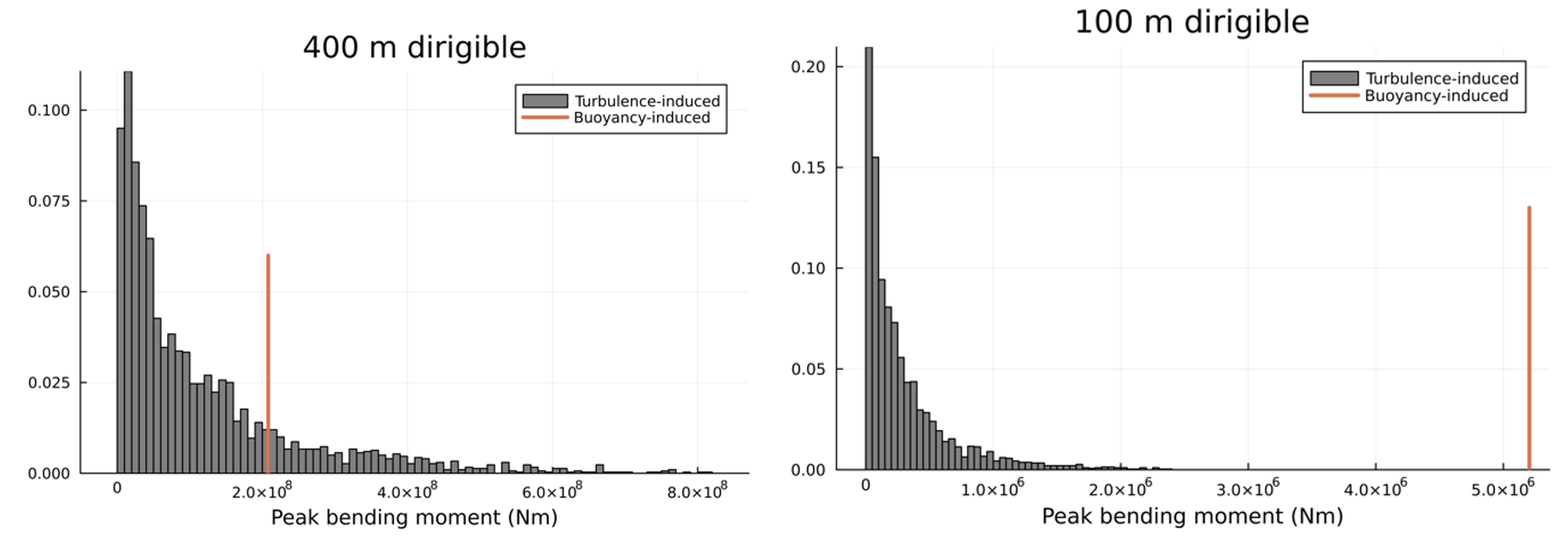
For a 100 meter dirigible, the bending moment imposed by the wind never comes close to exceeding the normal buoyancy-induced load on the structure (not once in the 3000 Monte Carlo runs that generated these plots). But for a 400 meter dirigible, the bending induced by the wind alone – a force that doesn’t depend on the loading or any revenue characteristic of the vehicle – exceeds the buoyancy-induced load about 17% of the time and occasionally exceeds the buoyancy-induced loads by a factor of 4. So an airship would need to be built substantially beefier (with correspondingly higher material cost and lower useful load) to reach even 400m in total length^[7]. For the operator who makes money on how far, how heavy, and how fast their aircraft travel, an airframe cost with an exquisite sensitivity to assumed weather is a new kind of fragility.

If one were to immodestly and irresponsibly abuse the scaling relations examined here, it’d go something like this: 1928’s Graf Zeppelin was 237m long and had a capacity of about 80 tons. If atmospheric correlation lengths cap the length of a buoyant air vehicle at ~400m, as they seem to, then the max cargo capacity for any similarly designed air vehicle is probably on the order of (400m/237m)³*80tons  ≈ 400 tons. With new materials and techniques, round it up to ~500ton cargo, 1000 ton gross. That’s a size that looks economical for some applications—but sadly, it's probably a limit, not merely the starting point for a buoyant new future.

There might be ways around this size limit. Turbulence avoidance is one. Regulatory requirements around aircraft design (like the turbulence models discussed here) reflect that the constraints on the physical aircraft are linked to expectations for the decisionmaking system^[8] that operates it. Decisionmaking systems and the information available to them have gotten much better in the many decades since the last commercial airships were certified to operate. With the right advance knowledge, perhaps giant airships could predict and sidestep turbulent regions that would otherwise tear them apart.

More speculatively, active turbulence neutralization might be another way to ‘push the envelope’ on the maximum size of an airship. Eli Dourado brought this up after recalling how in Neal Stephenson’s Atmosphaera Incognita, a giant tower is kept from being torn apart in the wind by turbofan engines mounted along it^[9].  

It might not be all sci-fi. Big airliners already do something like this—widebody transport aircraft from the C-5 [12] to the 787 use their control surfaces to respond to gusts in real time—and some newer concepts even measure incoming gusts before they arrive via doppler anemometry. That gives passengers a smoother ride and alleviates structural loads to prolong the airframes’ fatigue lives. In the Neal Stephenson variation on this trick, an airship with vector-able distributed propulsion (tiny propellers all over the thing) might be able to spin those propellers to actively counteract gust loads as they arrive. Consider for comparison a large 15MW wind turbine, which might use a 250m rotor to extract about a third of the energy from the airflow through a 50,000m² disc. A 400m airship might present about the same surface area as the wind turbine in profile, and have a powerplant of perhaps 15MW max. So from an energetic standpoint, it’s not impossible that individual propellers could point into the wind to meaningfully relieve some turbulence loads in real time^[10]. 

Wrapping up, we’re not trying say that autonomous cargo airships won’t or can’t happen. In a world with more than 100 electric aviation startups, a reallocation of resources to look back at a category-breaking transport mode like airships might make sense. After all, a lot has changed since the 1930s—polymers, composites, autonomy, better weather forecasting etc.

Rather, we want to point out that without careful forethought, the same kinds of scaling laws that made Graf Zeppelin or the Hindenburg so big in the first place might also prohibit cargo airships from getting too much bigger than that even in the long run^[11]. Hopefully people will be realistic in the attainable tonnage and J/ton*km figures they advertise.  

‍